Lab 7

Arbitrary Function Generator

Introduction

In this project, you will implement an analog function generator with selectable square, triangle or sine wave output.

The project uses the peripheral module PMOD DA1.As a starting point, there is a pre-made VHDL control interface for this module (pmod_da1_ctrl.vhd) available for download from the course web page.

Documentation for the PMOD DA1 module (in PDF form) is also available on the web page.

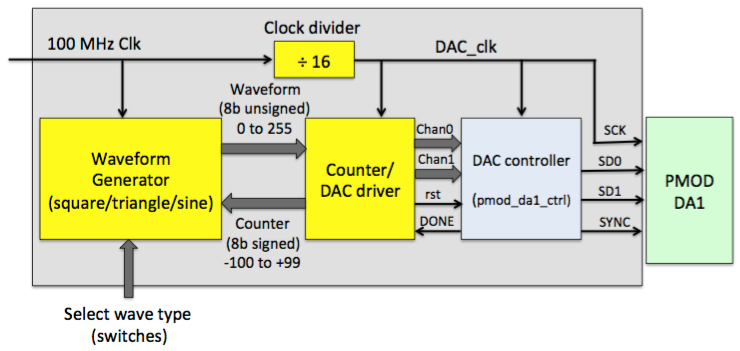
Design overview

A suggested design is shown in the above block diagram. Here, the functionality is divided between two main blocks. These may be implemented as separate VHDL components, or processes in the main architecture.

Waveform Generator: Receives an 8-bit signed counter value (range -100 to +99), and from that value calculates an 8-bit unsigned DAC output (range 0 to 255). The generator can produce square, triangle and sine wave forms, and user switches are used to select the desired output.
Counter/DAC driver: Receives the 8-bit unsigned output from the Waveform Generator, and transfers it to pmod_da1_ctrl using a simple protocol. This functional block also contains the 8-bit signed counter that drives the input of the Waveform Generator. The counter is incremented once per write cycle to the DAC.

The Waveform Generator can (and should) run at the 100 MHz system clock rate. The PMOD_DA1 cannot run at higher than 25 MHz, and the BASYS3 PMOD pins have additional limitations, so a clock divider is necessary to produce a slower DAC_clk. This slow clock also drives the pmod_da1_ctrl component and the Counter/DAC driver block.

For simplicity, the output frequency and amplitude can be fixed to single values. More details are given in the following sections.

Waveform generator

The waveform generator receives a single 8-bit signed "X" input with range -100 to -99, and produces a corresponding "Y" value (8 bit std_logic_vector in unsigned notation) for a square wave, triangle wave, and sine (or cosine) wave at that value of "X". The desired "Y" value is selected for output by some combination of user switch inputs. You can decide the best way to implement this interface. You may also implement the different waveforms as you like, but the following are some suggestions for how this could be done.

Square wave

A square wave is trivial to implement. Since the counter input range is -100 to +99, one simple approach would to set the output value low (0) if X is negative, and high (255) if X is positive.

Triangle wave

The triangle wave is slightly more complicated to produce than the square wave, because it has a continuously rising value for half of the cycle, and a falling value for the other half.

You can still take advantage of the fact that the counter input alternates between negative and positive. For instance, a simple triangle wave can be made by setting Y=X when X is positive, and Y=100+X when X is negative. Convert the result to an 8-bit std_logic_vector.

This strategy will create an output range of only 0-100 (the full scale is 255), which is less than ideal. You can easily multiply the output scale by 2 (0-200) by "left-shifting". In other words, truncate the MSB of the vector, and concatenate an extra '0' bit to the LSB end of the vector.

Sine (or cosine)

There is no native support in VHDL for trigonometric functions like sine and cosine, or for other complex math such as hyperbolic functions, square roots, etc. Calculations like these in digital logic can be slow and resource-hungry, and FPGA designers have different approaches for performing the calculations quickly and/or reducing the amount of necessary logic.

One approach is to use a memory lookup table implemented in block (or distributed) RAM, which is loaded with the desired function. The input "X" selects an address in the RAM, and the data contents at that address are output as the resultant "Y". This approach is the fastest and most flexible way to implement any arbitrary calculation.

If you prefer to use logic instead of RAM, CORDIC (Coordinate Rotation Digital Computer) algorithms are a good tool for implementing trigonometric, hyperbolic, square root or coordinate rotation calculations with a small amount of logic. In the Vivado IP Catalog, one can configure and generate a variety of custom CORDIC cores.

Implementing Sin/Cos as a cordic algorithm

In IP Catalog, navigate to the CORDIC IP and double-click on it to customize the core:

Under configuration options, select the following:
Functional Selection: Sin and Cos.
Architectural Configuration: Parallel. This option uses more logic, but produces a valid result every clock cycle.
Pipelining Mode: Maximum. This gives maximum timing performance, at the cost of more logic use
Phase Format: Radians.
Under input/output options:
Input Width: 8. Receives an 8-bit signed vector
Output Width: 8. Produces two 8-bit signed vectors (sin + cos) in a 16-bit vector
Round Mode: Truncate

Generate the core and instantiate it in your design. The input port s_axis_phase_tdata is a 7-bit signed vector that you can drive with the X value from your counter.

The output port m_axis_dout_tdata is a 16-bit vector, comprising two signed 8-bit vectors. Bits 7:0 correspond to cos(X), while bits 15:8 correspond to sin (X).

The two tvalid port signals in the CORDIC component are handshake signals that indicate when the input/output data values are valid. You should set the s_axis_phase_tvalid input bit to '1'. The s_axis_dout_tvalid output port can be ignored.

For the input range -100 to +100, the sin(X) and cos(X) output vectors have range -64 to +64. The range can be shifted up to 0-128 by adding +64 and converting the result to an 8-bit std_logic_vector.

Like the triangle wave above, this unfortunately only covers half of the DAC output range. You can double the amplitude with a "left shift" operation here as well, but doubling the top value of 128 gives 256, which exceeds the 8-bit unsigned range 0-255. To prevent the unsigned output from "rolling over", you would need to add some extra logic to make the maximum output eqal to 255.

Counter/DAC driver

This functional block is driven by the slower DAC clock, and performs the dual functions of incrementing the value of "X" sent to the waveform generator, and sending the waveform output to the DAC via the pmod_da1_ctrl component. It can be implemented as a relatively simple state machine, dependent on the DAC clock and the DONE signal from pmod_da1_ctrl.

Important: The timing protocol of the PMOD DA1 module uses the falling edge of the serial clock, so it is best to operate this state machine on the falling clock edge as well.

The state machine should include the following steps:

Wait for the DONE signal from pmod_da1_ctrl to go high before writing a new value to the DAC.
Store the waveform generator output in a register, and set the 8-bit Chan0 and Chan1 outputs to pmod_da1_ctrl accordingly. This is best done before the waveform generator is sent a new value of "X".
Increment the "X" counter output to the waveform generator. If the previous counter value was 99, reset the counter to -100. It is best to do this before starting the DAC write process, so that the waveform generator has enough time to produce new output values.
Start the DAC write process by setting rst to '1' for one clock cycle.
Set rst to '0' again, and wait for the DONE signal to go high...

Implementing and testing the full design

The clock divider can be implemented either as a counter-based module written in VHDL, or as a multi-mode clock management (MMCM) tile that you can configure and generate in IP Catalog with the Clocking Wizard.

When simulating the different waveforms, it is possible (and helpful!) to display them as "analog" values in the wave window.

The top level design should receive the 100 MHz on-board oscillator clock and some user-switches for setting the generator output waveform. The PMOD DA1 module can be plugged into the PMOD port of your choice; consult the BASYS3 user manual to find the corresponding I/O pins for SCK, SD0, SD1 and SYNC.

Configure your board and measure the DAC output(s) with an oscilloscope. If the design does not work immediately, you can examine the SCK, SD0/1 and SYNC waveforms to see if they are functioning as they should.

When you have a working design, show your code and results to the instructor.